产品名称：【特别推荐】Dotmatics Graphpad

生产厂商：Dotmatics产品类别：其他软件

Dotmatics Graphpad Prism专为科学研究而构建的首选分析和图形化解决方案。这是一款在生命科学研究领域，尤其是生物学、药理学和医学研究中无处不在的权威软件。它被广大科研人员誉为“生物学的黄金标准”数据分析工具。

GraphPad Prism 是一款集生物统计学分析、科学绘图（可视化）、数据整理和科研报告于一体的综合性桌面软件。它的核心理念是：为科学家（而非专业统计学家或程序员）设计，让复杂的数据分析变得直观、准确且高效。它不是一款通用的编程工具（如 Python/R），也不是一个简单的绘图工具（如 Excel），而是专门为实验科学研究量身定制的“一站式”解决方案。

功能特征

·        有效组织数据-Prism 专门针对您要运行的分析进行格式化，包括定量和分类数据的分析。这使得正确输入数据、选择合适的分析以及创建令人惊叹的图表变得更加容易。

·        样本量和功效分析-过准确确定预测效应所需的样本量，从一开始就优化您的实验，或者在样本量有限的情况下研究您可以检测到的最小效应。简化您的研究流程，节省宝贵的资源，并提高研究结果的可靠性。

·        执行正确的分析-避免使用统计术语。Prism 以清晰的语言提供了一个广泛的分析库，从常见到高度特异性——t 检验、单向、双向和三因素方差分析、线性和非线性回归剂量反应曲线、二元逻辑回归、生存分析、主成分分析等等。每个分析都有一个清单，可帮助您了解所需的统计假设并确认您已选择适当的检验。

·        随时获取可作的帮助-降低统计的复杂性。Prism 的在线帮助超出了您的预期。几乎在每一步中，都可以访问 Prism 用户指南中的数千页。通过 Prism Academy 从视频课程、指南和教育材料中学习。浏览图表组合，了解如何制作各种图表类型。教程数据集还可以帮助您了解为什么应该执行某些分析以及如何解释结果。

·        一键回归分析-没有其他程序能像 Prism 那样简化曲线拟合。选择一个方程，Prism 会完成剩下的工作——拟合曲线，显示结果和函数参数表，在图表上绘制曲线，并插值未知值。专注于您的研究，而不是您的软件-Prism 为您处理编码。图表和结果会自动实时更新。对数据和分析的任何更改（直接输入数据、省略错误数据、纠正拼写错误或更改分析选择）都会立即反映在结果、图表和布局中。

·        无需编程即可自动执行工作-只需单击一下，即可自动将多个成对比较添加到您的分析中。要查看这些行和星号的自定义选项，只需再次单击工具栏按钮即可。对数据或分析进行调整，图表上显示的结果将自动更新。

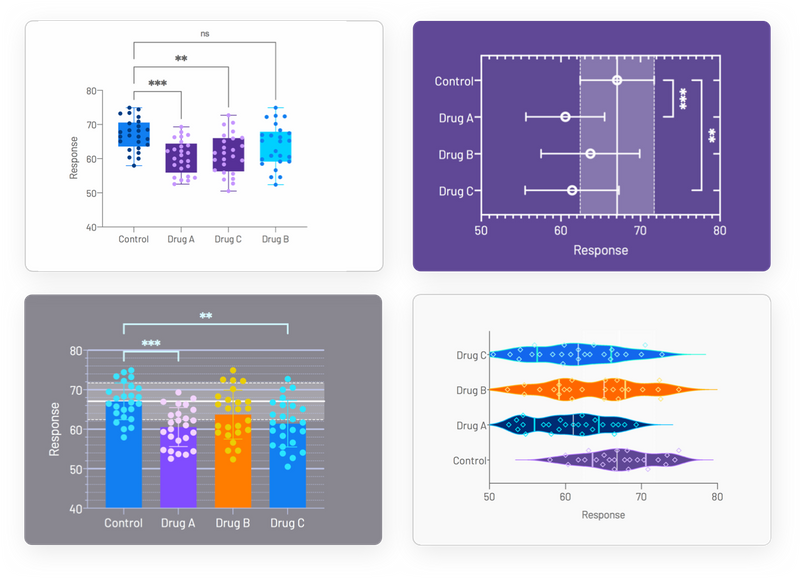
·        自定义图表的无数种方法-探索呈现单个数据集的无数种方法。选择最清楚地讲述数据中包含的故事的可视化样式。只需选择一种图表类型，然后通过更改数据排列方式、数据点样式、标签、字体、颜色等进行实时自定义。定制选项是无穷无尽的。

·        探索您的数据-将精力集中在分析最相关的数据上。自定义在数据中呈现关系的方式，以有效地探索大型数据集。注意到一些有趣的事情了吗？突出显示单个数据点以探索其相应的属性。借助 Prisms 强大的数据整理功能，您既可以节省时间，又可以确保您的分析基于干净且结构良好的数据。

·        一键导出出版物质量的图表-缩短发布时间。Prism 允许您自定义导出（文件类型、分辨率、透明度、尺寸、色彩空间 RGB/CMYK）以满足期刊的要求。设置默认值以节省时间。

·        协作、简化-避免那些混乱的电子邮件线程，并使用 Prism Cloud 共享、查看和协作处理您的 Prism 项目。使用 Prism 的开放访问文件格式保护结果的互作性和可重用性。通过使用行业标准格式（CSV、PNG、JSON 等），您可以确保您的项目可以在 Prism 之外使用，从而为您的数据工作流程和集成开辟新的可能性。

数据表类型

·        XY 表-当每个数据点都由单个 X 和 Y 值定义时使用。这些类型的数据通常与线性或非线性回归模型拟合。

·        列表-用于按单个分组变量组织成组的数据（例如，治疗变量与对照组或女性变量与男性）。通常使用 t 检验和单因素方差分析进行分析。

·        分组表-用于按两个分组变量（例如，女性对照与女性治疗与男性对照）分组的数据。通常使用双向方差分析进行分析。

·        列联表-用于按两个分组变量（治疗与对照和阳性与阴性结果）分组的计数数据。适用于卡方和费舍尔精确检验分析。

·        生存表-用于进行 Kaplan-Meier 生存分析。每一行代表一个受试者或个体，具有经过的生存时间和结果。

·        饼图-当询问“表中的每个值占总数的多少”时使用。用于计算分数和生成饼图。

·        多变量表-当数据的每一行是不同的观测值，并且每列都是不同的变量并支持文本值时使用。可以直接使用多元线性回归、Cox 回归等进行分析，也可以重组为 Prism 的其他表类型之一。

·        嵌套表-当数据组织成分层组时使用。使用嵌套 t 检验或嵌套单因素方差分析进行分析。